某次面试

发表于 更新于 分类于
本文字数： 1.4k 阅读时长 ≈ 1 分钟
记录某次面试题

三面报告

简单尝试

1
2
c=2857831458617919915448348973202449428172975402344447845149753833225
n=108607598680742993231063442886639267104372363777255285964116381103517303965067

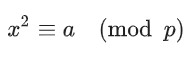
avatar

看着识字感觉有点熟悉，类似与RSA的低加密指数分解攻击，试一下

1
2
3
4
5
6
7
8
9
10
11
12
import gmpy2
from Crypto.Util.number import *
c = 2857831458617919915448348973202449428172975402344447845149753833225
n = 108607598680742993231063442886639267104372363777255285964116381103517303965067

m = gmpy2.iroot(c,2)
#(mpz(1690512188248851376925542155690365), True)
#另一解n- m[0]
#108607598680742993231063442886639267104372362086743097715265004177975148274702
print(long_to_bytes(m[0]))
#b'SYC{good_job!}'
print(long_to_bytes(n-m[0]))

在思考一下，和RSA的低加密指数分解攻击有点类似的Rabin算法（是一种基于模平方和模平方根的非对称加密算法）。尝试用yafu，factordb分解n，失败。在验证一下n是不是素数。

1
2
print(isPrime(n))
#1

那就说明不是Rabin加密。

看提示要探索x背后的秘密，回想之前数论学习里面的二次同余式的知识，试一下。

二次剩余

一个数 a，如果不是p 的倍数且模 p同余于某个数的平方，则称 a为模p 的 二次剩余 。而一个不是 p的倍数的数 b，不同余于任何数的平方，则b称 为模 p的 非二次剩余 。

是否有解

引入勒让德符号

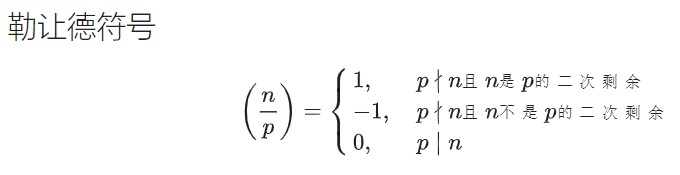
avatar

通过勒让德符号可以判断一个数 是否为二次剩余，具体判断 是否为 的二次剩余，需要通过欧拉判别准则来实现

欧拉判别准则

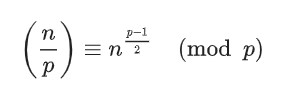
avatar

证明：avatar

Cipolla算法

Cipolla算法是解决二次剩余强有力的工具，一个脑洞大开的算法

证明

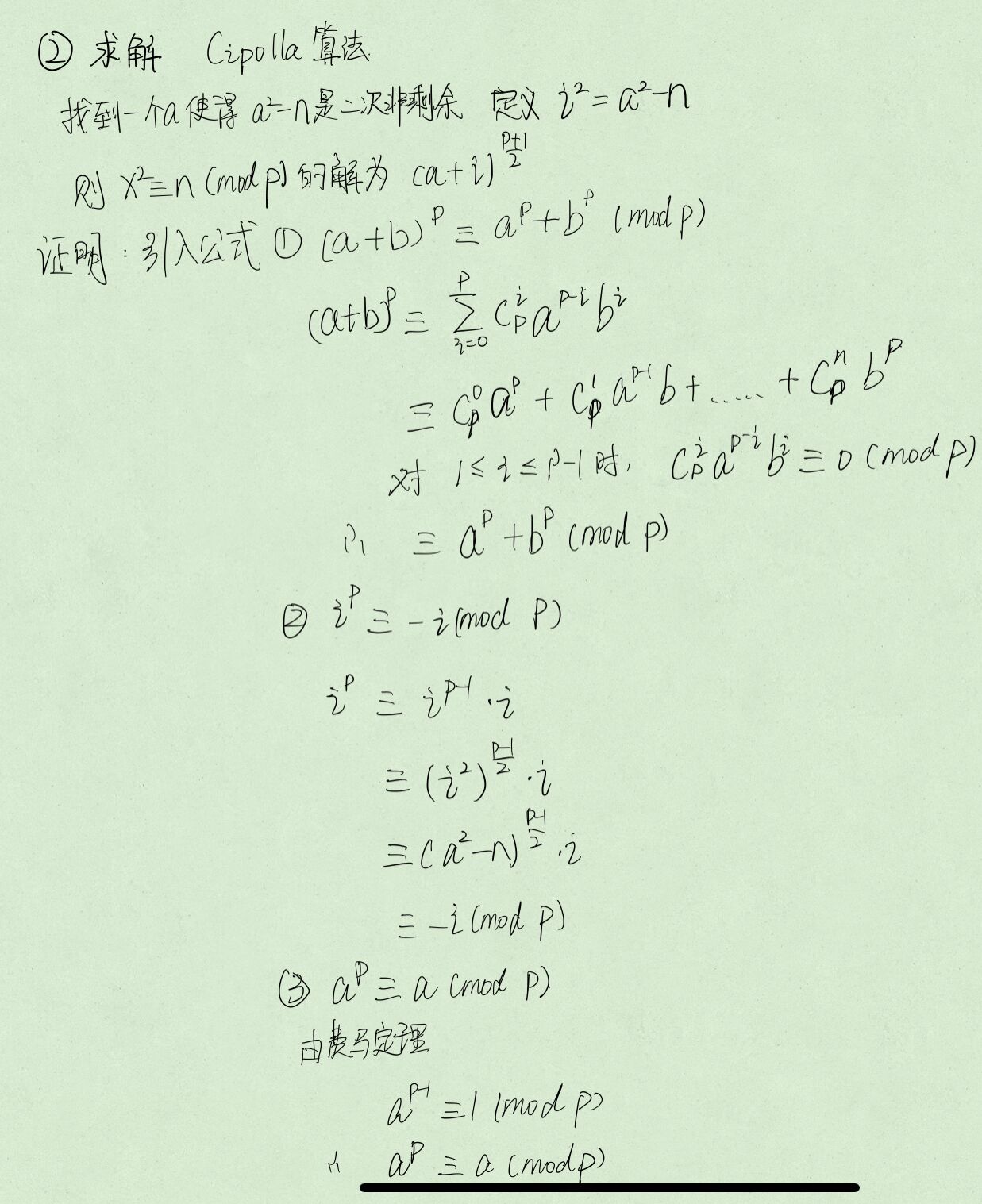
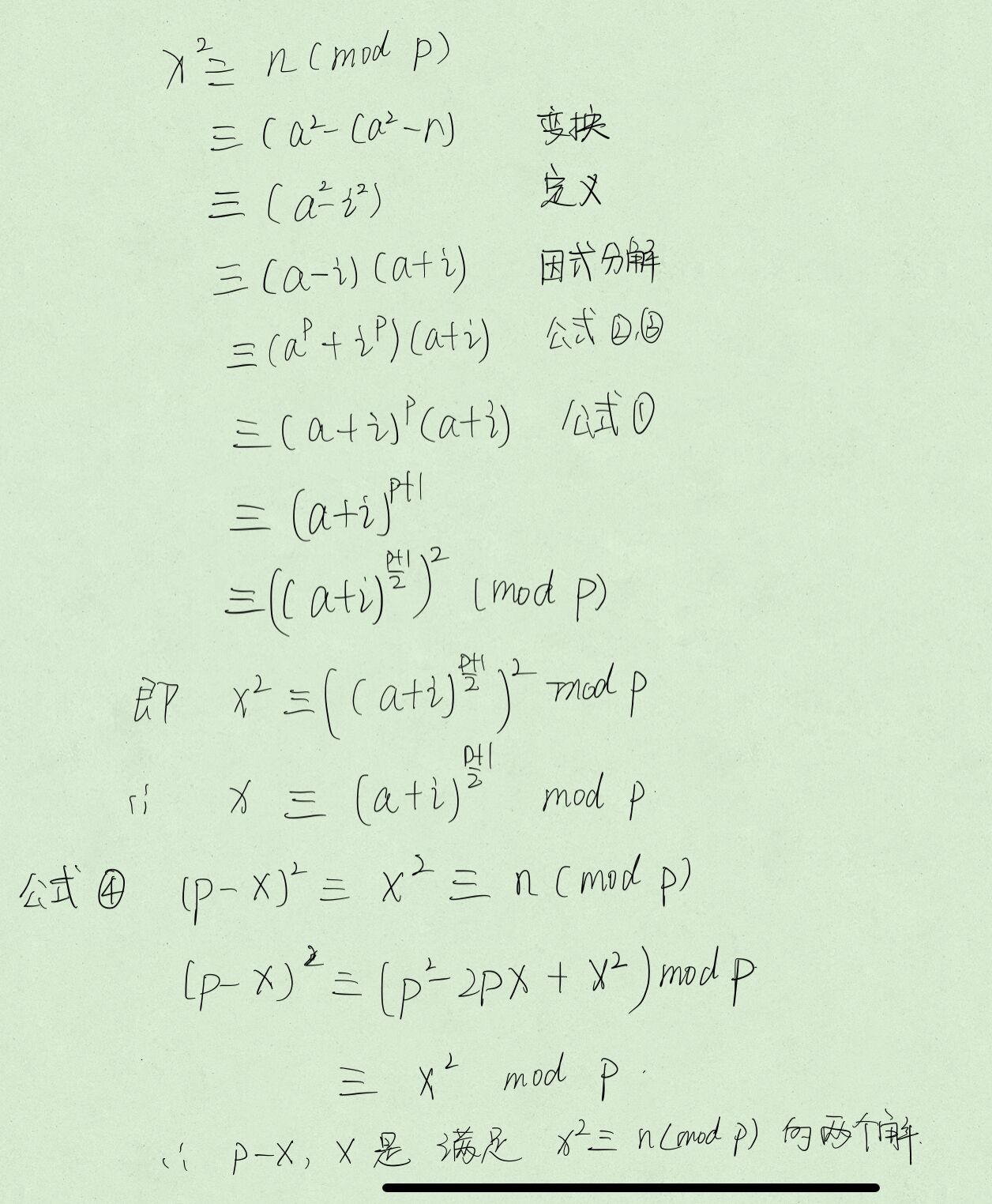
avater

avater

代码实现

1
2
3
4
5
6
7
8
9
10
11
c = 2857831458617919915448348973202449428172975402344447845149753833225
n = 108607598680742993231063442886639267104372363777255285964116381103517303965067

while(1):
    a = random.randint(1,n)
    i=a*a - c
    if(gmpy2.legendre(i,n) == -1):
        i_sqrt = gmpy2.sqrt(i)
        break;
x = gmpy2.powmod(a+i_sqrt,n+1//2,n)
print(x,-x%n)

非预期解

1
2
3
if (n % 4 == 3):
    ans = pow(c, (n + 1) // 4, n)
    print(ans, -ans % n)