零知识证明初探
简介
零知识证明技术是现代密码学三大基础之一,由 S.Goldwasser、S.Micali 及 C.Rackoff 在 20 世纪 80 年代初提出。早期的零知识证明由于其效率和可用性等限制,未得到很好的利用,仅停留在理论层面。直到近年来,零知识证明的理论研究才开始不断突破,同时区块链也为零知识证明创造了大展拳脚的机会,因而走进大众视野。
数独的故事
数独大家都很熟悉, 玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并
满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复 。
——以下简称数独规则
数独盘面是个九宫,每一宫又分为九个小格。 在这八十一格中给出一定的已知数字和解题条件,利用逻辑和推理,在其他的空格上填入1-9的数字。
现在有一个问题,假如我知道某个数独的答案,如何向张三证明我有答案。
诚然,最简单的方法是把答案给张三看。张三就能通过校验来判断我是否有答案。但是这带来一个风险,如果我和张三之间存在交易,张三知道答案之后不愿意付相应的报酬,这就会对我产生损失。这就带来另外一个问题。
如何在不给张三看答案的情况下,证明我有答案。
简单建立一个思路,给张三直接看答案也是让其检验答案满足数独规则,如果能够证明我的数独满足规则,也就间接证明我有答案。所以我把多个完整的数独拆分成九行,九列,九个九宫格,然后打乱装进袋子里。
然后让张三选择验证行,验证列,验证九宫格。张三选择按照行来验证,他打开九个袋子,发现上面的数字都满足数独规则。此时张三发现,我可以刻意构造一种满足的序列来欺骗他。我急忙解释:但是我事先不知道你会选择行还是选择列抑或是九宫格。张三要求多次验证,经过多次验证,发现我提供的都满足数独规则,张三将信将疑的选择相信我有数独的答案。
当然,细推上面的故事,会发现很多漏洞,比如
张三可以根据其中的一个正确答案去反推出他需要的答案,只要知道的数字足够,完完全全可以降低推理的难度。
我也可以伪造一个完全不是该数独的答案,以此来蒙骗张三。
这些并不是重点,重点在于这个故事可以让大家对零知识证明有一个大致的印象。零知识证明的本质就是在不揭晓我所知道或拥有的某样东西的前提下,向别人证明我有很大几率确实知道或拥有这个东西。
这点和某些加密算法的思想很类似,RSA的公钥破解在理论上是可行的,但是在现实中被破解的概率非常小就能保证该密码算法的安全性。再比如哈希算法,一定存在多个输入对应一个输出,但是在现实中我们很难找到第二个输入去对应一个已知的输出。这难道就是概率学?
地图三着色问题
三色问题是如何用三种颜色染色一个地图,保证任意两个相邻的地区都是不同的颜色。我们把这个地图三染色问题转变成一个连通图的顶点三染色问题,假设每个地区都有一个首府(节点),然后把相邻的节点连接起来,这样地图染色问题可以变成一个连通图的顶点染色问题。
下面的问题就是已知一个确定的连通图,如何不公布结果的情况下证明我知道染色的方案。假设连通图是下图所示
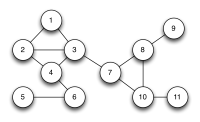
如果你曾经看过任何加密相关文章,你可能知道,解决这种困境的正确方法,就是想出一个绝对疯狂的技术手段 。
用帽子🎩!!!
下面简述运作原理,我在一张空白的纸上画出带有着色方案的连通图,然后在每个节点上面盖上帽子。此时的张三并允许选择任意一条边,我就会将改边对应的两个顶点的帽子揭开展示给张三看,确实是不同的颜色。这也只能证明我可能没有撒谎。张三认为他只进行了一轮的观察,不足以完全相信我。假设有E条边,张三受骗的概率[(E-1)/E] * [(E-1)/E],这是非常高的。所以需要多次验证,保证受骗的概率降到极低。经过E^2验证之后,可以将受骗概率降到极低。当然每一次验证我都会随机更换成另外三种颜色,防止张三通过验证前后串起来从而得到所有的答案。一个据此设计的在线demo
但是你可能会有疑问,这个问题似乎没有什么现实的意义。让我们来一步一步探索。
地图三着色问题属于NP问题)(非确定性多项式难题),是指一个复杂问题不能确定是否在多项式时间内找到答案,但是可以在多项式时间内验证答案是否正确。最有趣的地方再有三色问题是一个NPC(Non-deterministic Polynomial Complete)问题。
建议阅读这篇文章,也就是说我们任何其他属于这一类的NP问题都可以转化为这个问题的实例。那在现实什么问题属于这类NP问题呢,比如分配蜂窝网格,要求每两个电塔不具有相同波段,避免信号📶干扰,但是电塔只允许传播三种波段的信号,此时我们就可以转化为上述的三色问题进行解决。更多有趣的内容在论文
P=NP?
证明P=NP同时也是千禧年大奖难题之一
NPC问题存在着一个令人惊讶的性质,即如果一个NPC问题存在多项式时间的算法,则所有的NP问题都可以在多项式时间内求解,即P=NP成立!!目前已经发现3000+的NPC问题。
三个性质
完整性(completeness):V无法欺骗P。若P知道一个定理的证明方法,则P使V以绝对优势的概率相信他能证明。
可靠性(Soundness):P无法欺骗V。换言之,若P不知道一个定理的证明方法,则P使V相信他会证明定理的概率很低。
零知识性(Zero-knowledgeness):V无法获取任何额外的知识。
一个完备的零知识证明需要同时具备以上三种性质。其实也对应来三大难点,需要设计出能满足证明的方法,证明者在证明过程中不能作弊(方法不存在可以利用的缺陷或漏洞),验证者无法在证明过程中获取被证明对象的部分或完整内容(对证明者形成威胁)。